https://blog.csdn.net/u011630575/article/details/79409202
https://blog.csdn.net/weixin_47006934/article/details/106978071
https://developer.aliyun.com/article/504028
https://www.jiqizhixin.com/articles/2018-02-14-6
k-means 如何确定k 和 初始聚类
https://www.biaodianfu.com/hierarchical-clustering.html
K值确定
**法1：(轮廓系数)**在实际应用中，由于Kmean一般作为数据预处理，或者用于辅助分聚类贴标签。所以k一般不会设置很大。可以通过枚举，令k从2到一个固定值如10，在每个k值上重复运行数次kmeans(避免局部最优解)，并计算当前k的平均轮廓系数，最后选取轮廓系数最大的值对应的k作为最终的集群数目。
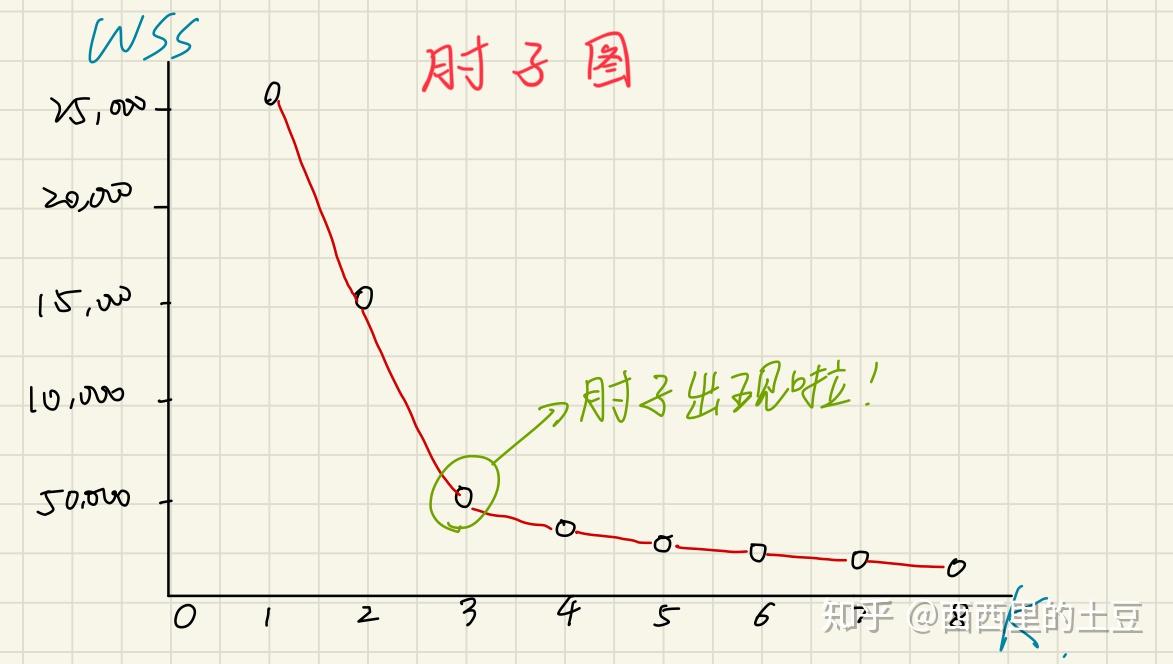
z常见的一种方法是elbow method，x轴为聚类的数量，y轴为WSS（within cluster sum of squares）也就是各个点到cluster中心的距离的平方的和。
法2：(Calinski-Harabasz准则)
其中SSB是类间方差，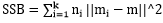
，m为所有点的中心点,mi为某类的中心点；
SSW是类内方差，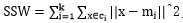
；
(N-k)/(k-1)是复杂度；
逻辑回归
1. 模型介绍
Logistic Regression 虽然被称为回归，但其实际上是分类模型，并常用于二分类。Logistic Regression 因其简单、可并行化、可解释强深受工业界喜爱。
Logistic 回归的本质是：假设数据服从这个分布，然后使用极大似然估计做参数的估计。
1.1 Logistic 分布
Logistic 分布是一种连续型的概率分布，其分布函数和密度函数分别为：
其中， 表示位置参数，
为形状参数。我们可以看下其图像特征：
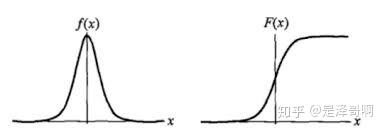
Logistic 分布是由其位置和尺度参数定义的连续分布。Logistic 分布的形状与正态分布的形状相似，但是 Logistic 分布的尾部更长，所以我们可以使用 Logistic 分布来建模比正态分布具有更长尾部和更高波峰的数据分布。在深度学习中常用到的 Sigmoid 函数就是 Logistic 的分布函数在 的特殊形式。
1.2 Logistic 回归
cluster聚合层次聚类算法
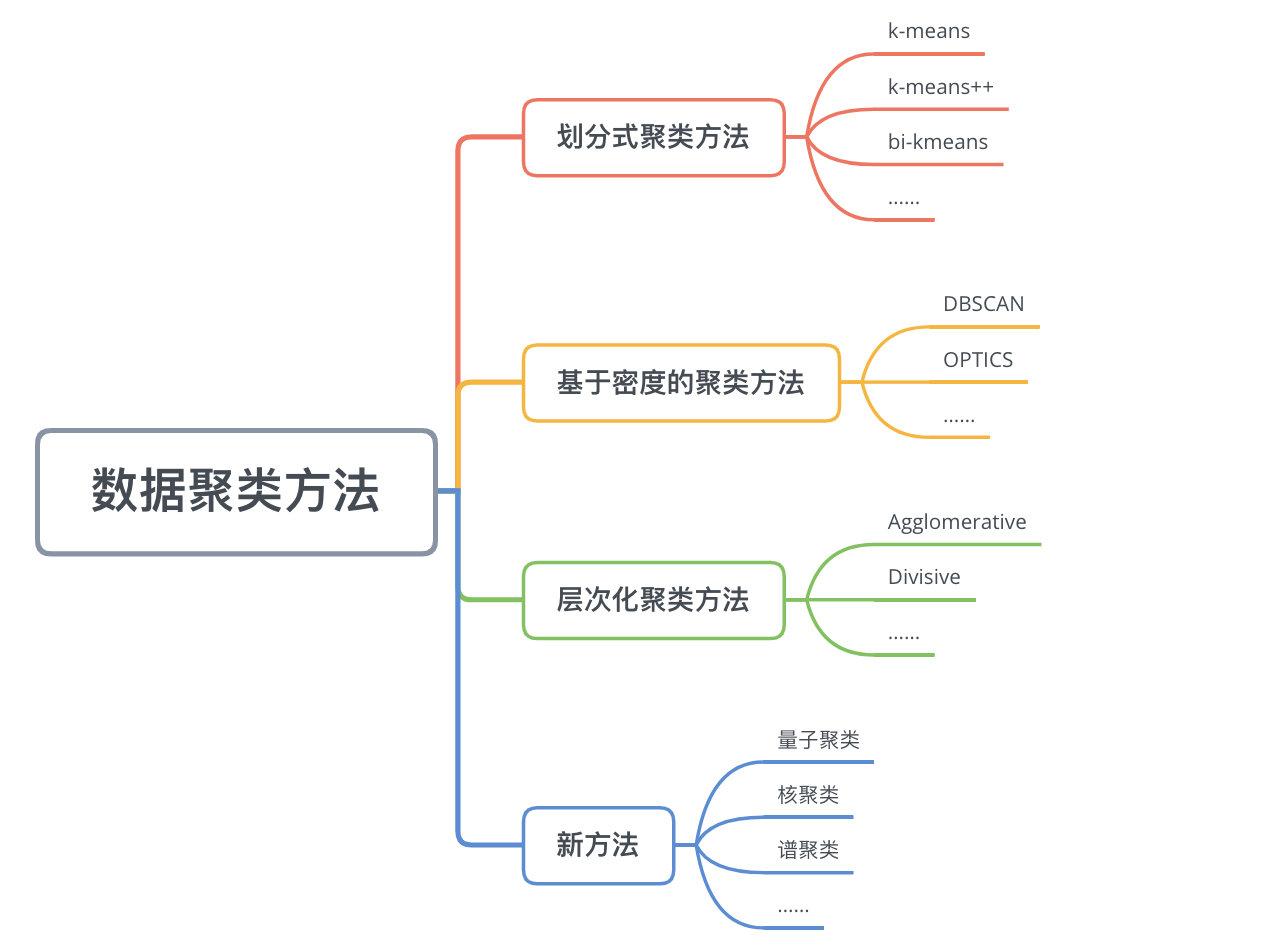
层次聚类通过对数据集在不同层次进行划分，从而形成树形的聚类结构。数据集的划分可采用“自底向上”的聚合（agglomerative）策略，也可采用“自顶向下”的分拆（divisive）策略。“自底而上”的算法开始时把每一个原始数据看作一个单一的聚类簇，然后不断聚合小的聚类簇成为大的聚类。“自顶向下”的算法开始把所有数据看作一个聚类，通过不断分割大的聚类直到每一个单一的数据都被划分。
根据聚类簇之间距离的计算方法的不同，层次聚类算法可以大致分为：单链接（Single-link）算法，全链接算法（complete-link）或均链接算法（average-link）。单链接算法用两个聚类簇中最近的样本距离作为两个簇之间的距离；而全链接使用计算两个聚类簇中最远的样本距离；均链接算法中两个聚类之间的距离由两个簇中所有的样本共同决定。
“自底向上”的聚合层次聚类算法
（1）计算任意两个数据之间的距离得到一个相似度矩阵（proximity matrix），并把每一个单一的数据看作是一个聚类；
（2）查找相似度矩阵中距离最小的两个聚类，把他们聚合为一个新的聚类，然后根据这个新的聚类重新计算相似度矩阵；
（3）重复（2）直到所有的数据都被归入到一个聚类中。
“自顶向下”的分拆（divisive）策略则与之相反。
active learning
主动学习（Active Learning）的大致思路就是：通过机器学习的方法获取到那些比较“难”分类的样本数据，让人工再次确认和审核，然后将人工标注得到的数据再次使用有监督学习模型或者半监督学习模型进行训练，逐步提升模型的效果，将人工经验融入机器学习的模型中。
那么主动学习（Active Learning）的整体思路究竟是怎样的呢？在机器学习的建模过程中，通常包括样本选择，模型训练，模型预测，模型更新这几个步骤。在主动学习这个领域则需要把标注候选集提取和人工标注这两个步骤加入整体流程，也就是：
- 机器学习模型：包括机器学习模型的训练和预测两部分；
- 待标注的数据候选集提取：依赖主动学习中的查询函数（Query Function）；
- 人工标注：专家经验或者业务经验的提炼；
- 获得候选集的标注数据：获得更有价值的样本数据；
- 机器学习模型的更新：通过增量学习或者重新学习的方式更新模型，从而将人工标注的数据融入机器学习模型中，提升模型效果
其中 L 是用于训练已标注的样本；
C 为一组或者一个算法模型，用户接收上一轮的标记样本集，通过负反馈调整模型参数，并输出对应的预测结果向量集；
Q 是查询函数，用于从当前剩余的未标注样本池（未标记样本会逐渐减少）U 中查询信息量最大（最不确定）的top样本；
S是督导者，可以为 U 中样本标注正确的标签；
active learning模型**通过少量初始标记样本 L 开始学习，通过一定的查询函数 Q 选择出一个或一批最有用的样本**，并向督导者询问标签，然后利用获得的新知识来训练分类器和进行下一轮查询。主动学习是一个循环的过程，直至达到某一停止准则为止。
需要注意的是，active learning是一个算法框架，上图中的单个模块具备可替换性（alternative）
图像校正(Image Rectification)
随机抽样一致算法（RANdom SAmple Consensus,RANSAC）
一、RANSAC介绍
随机抽样一致算法（RANdom SAmple Consensus,RANSAC）,采用迭代的方式从一组包含离群的被观测数据中估算出数学模型的参数。RANSAC算法假设数据中包含正确数据和异常数据（或称为噪声）。正确数据记为内点（inliers），异常数据记为外点（outliers）。同时RANSAC也假设，给定一组正确的数据，存在可以计算出符合这些数据的模型参数的方法。该算法核心思想就是随机性和假设性，随机性是根据正确数据出现概率去随机选取抽样数据，根据大数定律，随机性模拟可以近似得到正确结果。假设性是假设选取出的抽样数据都是正确数据，然后用这些正确数据通过问题满足的模型，去计算其他点，然后对这次结果进行一个评分。
二、算法基本思想
（1）要得到一个直线模型，需要两个点唯一确定一个直线方程。所以第一步随机选择两个点。
（2）通过这两个点，可以计算出这两个点所表示的模型方程y=ax+b。
（3）将所有的数据点套到这个模型中计算误差。
（4）找到所有满足误差阈值的点。
（5）然后我们再重复（1）~（4）这个过程，直到达到一定迭代次数后，选出那个被支持的最多的模型，作为问题的解。如下图所示
可以发现，虽然这个数据集中外点和内点的比例几乎相等，但是RANSAC算法还是能找到最合适的解。这个问题如果使用最小二乘法进行优化，由于噪声数据的干扰，我们得到的结果肯定是一个错误的结果，如下图所示。这是由于最小二乘法是一个将外点参与讨论的代价优化问题，而RANSAC是一个使用内点进行优化的问题。经实验验证，对于包含80%误差的数据集，RANSAC的效果远优于直接的最小二乘法。
